Kaye Jiale Li, Kinwah Wu, Ziri Younsi, Tjonnie G. F. Li

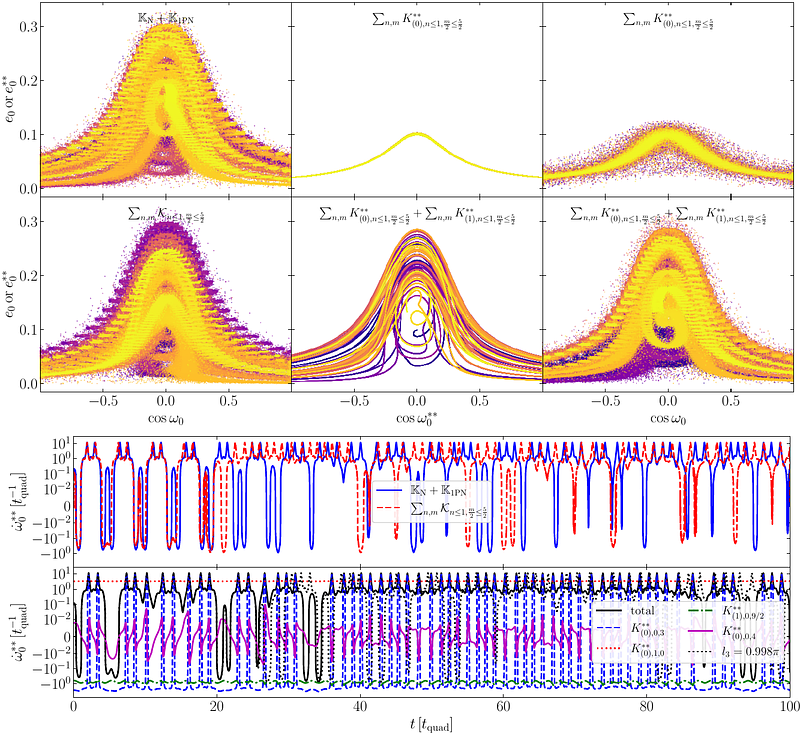
Relativistic secular perturbation theory has ignited significant interest in uncovering intricate cross-term effects, especially the interplay between 1PN and quadrupole terms. While most existing studies rely on the Lagrangian planetary perturbation method for computing cross terms, a comprehensive Hamiltonian framework for the field has been missing. In this work, we introduce a framework based on von Zeipel transformation, utilizing two sequential canonical transformations to systematically compute cross terms to arbitrary orders. Our results reveal secular cross terms up to quadrupole-squared order, showcasing remarkable consistency with both the Lagrangian method [1] and the effective-field-theory approach [2]. We present leading-order periodic cross terms arising from the interactions between 1PN and quadrupole, and present estimates of higher-order cross terms. It is demonstrated that this method not only accurately predicts the long-term evolution of hierarchical systems but also captures fast oscillations observed in N-body simulations. We identify and validate resonances caused by quadrupole-squared effects, highlighting both consistencies and discrepancies when compared to N-body simulations. These discrepancies underscore the importance of mean-motion resonances, a factor overlooked in current secular perturbation frameworks. Finally, we provide a comprehensive review of the subtleties and limitations inherent to secular perturbation theory, paving the way for future research and advancements in this field.