Aretaios Lalakos, Alexander Tchekhovskoy, Elias R. Most, Bart Ripperda, Koushik Chatterjee, Matthew Liska

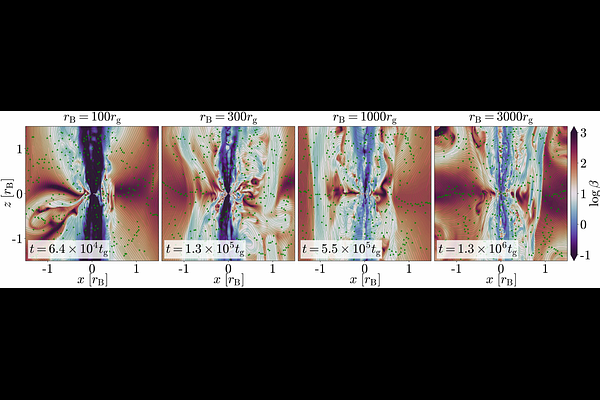
Accretion onto supermassive black holes (BHs) can launch relativistic jets that inject energy and momentum into their surroundings. Understanding how such feedback shapes large-scale accretion is key to bridging observations from galactic scales (e.g., the Bondi radius, $r_{\rm B}$) down to event horizon scales ($r_{\rm g}$), spanning 5-6 orders of magnitude. We tackle this challenge by varying the spatial scale separation across 2-4 orders of magnitude and performing some of the longest contiguous 3D general relativistic magnetohydrodynamic (GRMHD) simulations to date ($t \lesssim 4\times10^6 r_{\rm g}/c$), of Bondi-like accretion of rotating, non-relativistic gas with weak vertical magnetic fields onto a rapidly spinning BH, achieving inflow equilibrium out to $r \gtrsim 10^3 r_{\rm g}$. We find that, regardless of scale separation or ambient gas rotation, all simulations reach a magnetically arrested disk (MAD) state where the BH becomes magnetically saturated. In this state, the mass inflow rate follows a universal radial scaling: $\dot{M}_{\rm in}(r) \sim r^s$ with $s = 0.66 \pm 0.03$. The MAD state self-regulates through jets, outflows, and magnetic flux eruptions that can disrupt coherent angular momentum inflow, giving rise to a rocking accretion disk (RAD) state. This RAD state features chaotically oriented inflows, weak intermittent jets, and a steeper inflow slope of $s = 0.87 \pm 0.05$. The MAD and RAD BH accretion rates become comparable at typical scale separations, $r_{\rm B}/ r_{\rm g} \gtrsim 10^5$. Weaker RAD outflows allow large-scale inflows to resume, restoring the MAD state and enabling a recurring MAD-RAD cycle. These cycles can last tens of Bondi timescales, $t_{\rm B} \sim 0.2\,\text{Myr} \times (r_{\rm B}/10^{5} r_{\rm g})^{3/2} \times (M_{\rm BH}/10^9M_\odot)$, potentially setting the duty cycle of jetted AGN outbursts, such as in M87*.