Zacharaya Shabka, Michael Enrico, Nick Parsons, Georgios Zervas

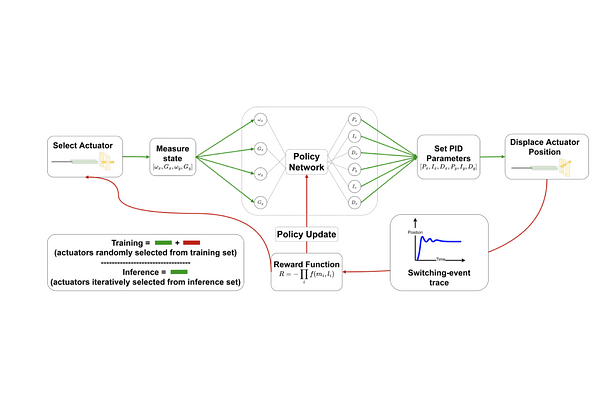
Proportional-integral-derivative (PID) control underlies more than $97\%$ of automated industrial processes. Controlling these processes effectively with respect to some specified set of performance goals requires finding an optimal set of PID parameters to moderate the PID loop. Tuning these parameters is a long and exhaustive process. A method (patent pending) based on deep reinforcement learning is presented that learns a relationship between generic system properties (e.g. resonance frequency), a multi-objective performance goal and optimal PID parameter values. Performance is demonstrated in the context of a real optical switching product of the foremost manufacturer of such devices globally. Switching is handled by piezoelectric actuators where switching time and optical loss are derived from the speed and stability of actuator-control processes respectively. The method achieves a $5\times$ improvement in the number of actuators that fall within the most challenging target switching speed, $\geq 20\%$ improvement in mean switching speed at the same optical loss and $\geq 75\%$ reduction in performance inconsistency when temperature varies between 5 and 73 degrees celcius. Furthermore, once trained (which takes $\mathcal{O}(hours)$), the model generates actuator-unique PID parameters in a one-shot inference process that takes $\mathcal{O}(ms)$ in comparison to up to $\mathcal{O}(week)$ required for conventional tuning methods, therefore accomplishing these performance improvements whilst achieving up to a $10^6\times$ speed-up. After training, the method can be applied entirely offline, incurring effectively zero optimisation-overhead in production.